Hexagonal Grids on a 2d Plane
- Sep 18, 2020
- 5 min read
Updated: Aug 21, 2021

In a previous post (8), I wrote about some of the properties of hexagons and how this shape occurs all through the natural world. Now I want to visit this again in relation to analysis on maps.
A digital image is a rectangular array of squares of color values called pixels which are mapped to square pixels of colored light coming from the surface of a monitor. When monitors first came out their pixels were not square but a 3:4 ratio so when a drawn square rotated on the screen, it stretched and shrunk. This is not a square because a square doesn't change it's shape when rotated. The terminology is that a square is invariant under rotation. Computer graphics programmers had to adjust for this when writing graphics software. Apple was the first commercial company to come out with square pixels with the introduction of a purely graphics-based desktop for the Macintosh computer in 1984. A raster is a digital image in which each pixel is called a cell. A cell can have one or a whole set of values called attributes, each of which can be colorized. The center of a cell also has a location on a surface based on the coordinate system of the surface and a size based on whatever measurement system applies. Cells also have a location based on their location on the raster, usually Cartesian coordinates with the origin (0, 0) being at the upper left or lower left corner of the raster. Rasters are an important way to view a map along with other structured graphics such a points, lines and polygons. Rasters are also used in spatial analysis; nearest neighbor, distance, spatial statistics, and visualization.

Von Neumann and Moore Neighborhoods (1)
There are three ways to completely cover a plane with one shape, called tessellations, they are squares, triangles and hexagons. A hexagonal tessellation is equivalent to a triangular tessellation with equilateral triangles. Neighbors of a square in a square grid have two different forms: the Von Neumann neighborhood (named after John Von Neumann in his first description of cellular automata) which is the four squares directly east, west and north south of the central square. Von Neumann neighborhoods use a Manhattan metric, measurement is like walking along a city block with no diagonals. The other is the Moore neighborhood after Edward F. Moore, a pioneer in cellular automata. John Conway's Game of Life was one of the first to use this neighborhood (3). A cell has eight neighbors and both straight and diagonal distances means that measurement is more problematic. A hexagonal grid has six hexagonal neighbors and distance between neighbors is the same. There is no special name for this neighborhood. If one measures distance between two points using the three neighborhoods, a hexagonal neighborhood diverges from a direct Euclidean measure by the least amount.

Connectivity in Von Neumann, Hexagonal, and Moore Neighborhoods (1)
If one looks at the connectivity between a single cell and it's adjacent cells, the adjacent cells connect once for a Von Neumann neighborhood, twice for a hexagonal neighborhood and three times for a Moore neighborhood. How does a hexagonal neighborhood change the results in The Game of Life? I found a version (6) using a hexagonal grid. Looks like some structures may be missing but other structures are quite rich. I couldn't find any interesting papers that weren't behind a paywall.
Square cells fit nicely onto a Cartesian coordinate system no matter what neighborhood they use. 2D cells require two coordinates and two axis. The Cartesian system is nicely symmetric so for most uses only a quarter of the plane is used. This is why for most raster images the upper or lower left corner becomes the origin. For hexagons, to get the same symmetry benefits, three axis and three coordinates are needed. I haven't seen any examples that actually use this system.

Hexagonal coordinates (1)
One particularly strong use of hexagonal grids is in visualization. Rasters containing a great deal of different elements (heterogeneous) are easier to read on a hexagonal grid as opposed to a square grid. This is why maps in many computer games use a hexagonal grid.
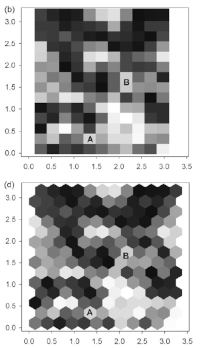
Visualization is square vs hexagonal grids (1)
The information I have found comes from a single paper (1) concerning a single discipline, ecology. The authors show that most researchers use a square grid. They also state that for models using partial differential equations (PDE): diffusion and flow, a square grid is required. Solutions to these equations require what are called boundary conditions, the boundaries of some arbitrary patch of space that the equations are solved on. These boundaries can be of any dimension. The simplest boundary conditions are called Neumann boundaries after Karl Friedrich Neumann (1793-1870) and the patch is assumed to be a square in 2D and equivalent to a Von Neumann neighborhood. This requirement of a square neighborhood turns out not to be true as I have found at least two papers showing how to numerically calculate PDEs using hexagonal boundary conditions (4)(5). If this is useful or practical or not is unknown.
In GIS, both ArcGIS Pro and QGIS allow for the creation of hexagonal tessellations (2)(7). Whether one is going from a raster image or binning a set of points it is important to note that this is a smoothing problem and edge effects between cells need to be addressed as there will be a lowering of resolution. The hexagonal cells will always be bigger than what you start with.
I find that for certain types of visualization using hexagons is striking. The rest is much murkier as to advantage. Having a choice of neighborhoods with square cells does create problems especially when some rasters represent boundaries. If a Moore neighborhood doesn't work but one still needs the extra connectivity then maybe a hexagonal grid is the way to go. Looking at what I've found for this post I see a great deal of research potential.

Black cells form a closed ring in a Von Neumann neighborhood.
In a Moore neighborhood the cells still form a closed ring
but don't enclose the neighborhood (1).
Birch, Colin P.D., Sander P. Oom, and Jonathan A. Beecham. “Rectangular and Hexagonal Grids Used for Observation, Experiment and Simulation in Ecology.” Ecological Modelling 206, no. 3–4 (August 2007): 347–59. https://doi.org/10.1016/j.ecolmodel.2007.03.041.
“Generate Tessellation (Data Management)—ArcGIS Pro | Documentation.” Accessed September 12, 2020. https://pro.arcgis.com/en/pro-app/tool-reference/data-management/generatetesellation.htm.
Das, Debasis. “A Survey on Cellular Automata and Its Applications.” Communications in Computer and Information Science. 269., 2011. https://doi.org/10.1007/978-3-642-29219-4_84.
Buranay, Suzan C., and Nouman Arshad. “Hexagonal Grid Approximation of the Solution of the Heat Equation on Special Polygons.” Advances in Difference Equations 2020, no. 1 (June 23, 2020): 309. https://doi.org/10.1186/s13662-020-02749-z.
Lee, D., H.C. Tien, C.P. Luo, and H.-N. Luk. “Hexagonal Grid Methods with Applications to Partial Differential Equations.” International Journal of Computer Mathematics 91, no. 9 (September 2, 2014): 1986–2009. https://doi.org/10.1080/00207160.2013.864392.
r/gameoflife. “Game of Life on a Hexagonal Grid.” reddit. Accessed September 16, 2020. https://www.reddit.com/r/gameoflife/comments/2n1t6g/game_of_life_on_a_hexagonal_grid/.
Dempsey, Caitlin. “Using QGIS to Create a Hexbin Map of GISP Registrations.” GIS Lounge (blog), February 21, 2017. https://www.gislounge.com/using-qgis-create-hexbin-map-gisp-registrations/.
Beaver, Bill. “Hexagons.” Emergent Thoughts, July 19, 2020. https://wjbeaver.wixsite.com/mysite/post/hexagons.



Comments