Hexagons
- Bill Beaver

- Jul 19, 2020
- 5 min read
Updated: Jun 24, 2022
Hexagons are everywhere in the natural world. Most people think of honeycomb when they think of hexagonal patterns but wasps also build hexagonal chambers for their young. Hexagonal patterns abound in insects. Arthropod eyes are constructed of columnar hexagonal cells and insect cuticle is laid down in hexagonal patterns. (7)(8) Semi-transparent cuticles laid down in offset hexagonal sheets give rise to the iridescent color in some insects like butterfly wings or the elytra of beetles. Iridescence also appears in the feathers of birds and the skin of fish and lizards. This is related to moire patterns, again produced by offset hexagonal grids. At a much smaller level, the basic structure of organic chemistry is the six-carbon atom benzene ring.

Honeycomb (5)

Insect Eye (3)
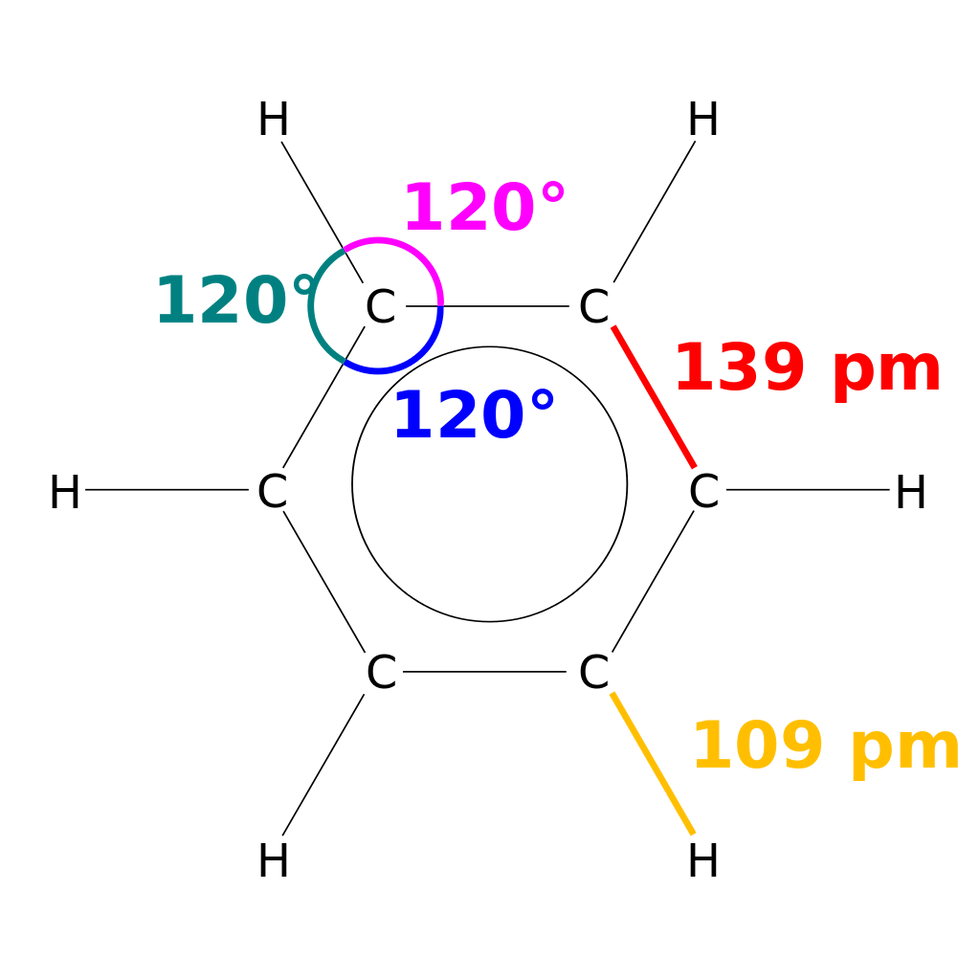
Benzene Ring (9)
Nonorganic physical processes also form hexagons. Boiling a liquid a certain way can create what are called closed Rayleigh-Binard convection cells on the surface of the liquid which have a hexagonal shape. (1) Basalt lava cooling a certain way has created hexagonal columns all over the world such as the Giant's Causeway in Ireland. (4) In geology, this process is called columnar jointing. In atmospheric science, hexagonal cloud patterns can appear, a process called evanescence.
The Cassini mission to Saturn explored the planet between 2004 and 2017. Saturn's year is 29 years long so the spacecraft witnessed a little less than half the planet's year. In May of 2017, the spacecraft took pictures of the north pole of the planet during the summer solstice. From May of 2013 to the end of the mission in August of 2017 a huge hexagonal cell formed over the north pole, reaching its most perfect form at the summer solstice and already starting to deteriorate 3 months later. Hexagonal patterns have also been found in storms on Jupiter but nothing so stable or perfect or at this high an altitude. (2)
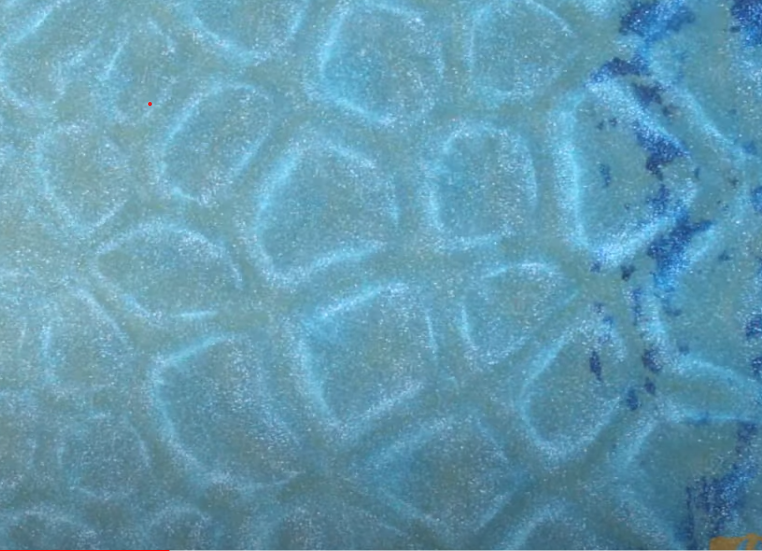
Convection Cells (1)

Giant's Causeway (4)

North Pole of Saturn (2)
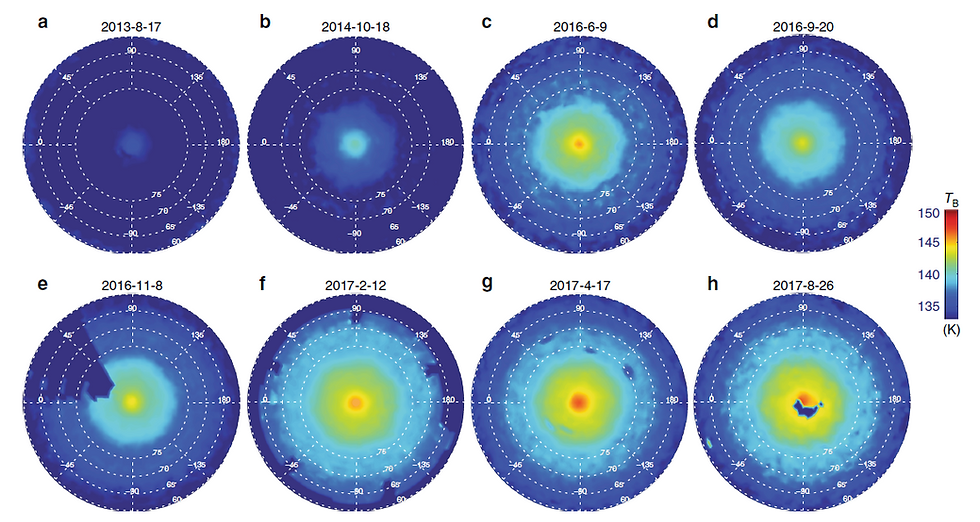
Formation of hexagonal convection cell over the north pole of Saturn (2)
I want to talk about hexagons as mathematical objects. Let us start with the number 6. 6 is the first perfect number. Perfect numbers are numbers where the sum of all its factors but itself equals the number. Here are the first three perfect numbers:
6 = 1+2+3
28 = 1+2+4+7+14
496= 1+2+4+8+16+31+62+124+248
Another feature of perfect numbers is multiplication. Perfect numbers use this rule:
1+2 = 3, 3*2 = 6
1+2+4 = 7, 7*4 = 28
1+2+4+8+16 = 31, 31*16 = 496
The sum of the factors up to the first odd prime equals the first prime. Multiply this by the last factor in the sum and this should equal the number.
No one knows whether there is an odd perfect number or if the set of perfect numbers is infinite. Because they use factors, perfect numbers are related to prime numbers. Like perfect numbers, no one knows whether the set of prime numbers is infinite and there is no formula that gives all prime numbers. Prime numbers form what is called a sparse set, there are fewer prime numbers the larger the number. In 1640, a French mathematician, Marin Mersenne, came up with a formula that he predicted would result in prime numbers:
n = a^p – 1, where n is not divisible by a and p is a prime factor of n.
Mersenne Numbers, however, do not predict primes every time but do create a less sparse set, allowing for the finding of primes in which the most modern computers would take centuries to calculate by brute force. This makes Mersenne Primes very valuable as they form the basis of modern cryptography. Mersenne's formula came from an earlier formula for perfect numbers:
2^(p − 1)(2^p − 1)
Perfect numbers are related to Mersenne Primes but the set of perfect numbers is much more sparse than primes. A computer can generate billions of small primes but there are only 51 known perfect numbers. Probably because of this, there is no known application for perfect numbers. (11)
Perfect numbers have been known since antiquity and the number 6 is the center of various spiritual theories as the sum and multiple of Unity, Duality, and Trinity. (10)
A regular hexagon is a six-sided closed object where all sides meet at an equal angle, 120 degrees. If the distance from the center of a hexagon to its vertices is 1 then the length of each edge is 1, so the distance from one vertex to its opposite is 2. Regular hexagons are one of three polygons that can cover (tile) a plane. The others are equilateral triangles and squares. A piece of a hexagonal tiling is called a hexagonal tessellation in 2D geometry and a hexagonal mesh in 3D. Circles inscribed inside a hexagonal tessellation are the most efficient way to pack like-sized circles. A hexagonal mesh like chicken wire does not deform as easily as a square mesh and uses fewer materials than a triangular mesh. All of these properties are behind the formation of honeycombs.
In 3D geometry, any surface can be classified as open or closed. Open surfaces can have curvature but topologically they are equivalent to a plane so they can be tiled with a hexagonal mesh. Closed surfaces such as the cylinder and the torus (doughnut) can be tiled with hexagons but a sphere cannot. A set of pentagons is needed (soccer balls.) (6)
Differential geometry is the geometry of continuously curved surfaces, both closed and open. These continuous surfaces can be made discrete and represented by a polygonal mesh. This is used in computer animation. The most efficient algorithms to do this, programs that run the fastest and use the least computer resources, use a non-regular hexagonal mesh as opposed to a rectangular or triangular one. (12)
I hope that I have shown that hexagons are important structures in geometry and the natural world. In future posts, I will try to show how hexagons arise out of non-linear dynamic models and how hexagonal patterns underlie our very thought processes.
Moore, Nick. Rayleigh–Bénard Convection Cells, 2016. https://www.youtube.com/watch?v=gSTNxS96fRg.
Fletcher, L. N., G. S. Orton, J. A. Sinclair, S. Guerlet, P. L. Read, A. Antuñano, R. K. Achterberg, et al. “A Hexagon in Saturn’s Northern Stratosphere Surrounding the Emerging Summertime Polar Vortex.” Nature Communications 9, no. 1 (September 3, 2018): 3564. https://doi.org/10.1038/s41467-018-06017-3.
Hooke, Robert. “Compound Eye of Gray Fly.” In Wikipedia, 1665. https://en.wikipedia.org/w/index.phptitle=File:Compoundeye.png&oldid=475195542.
Norris, Anna. “11 Beautiful Basalt Columns around the World.” From the Grapevine, 2014. https://www.fromthegrapevine.com/nature/11-intriguing-basalt-formations-around-world.
“Honeycomb.” In Wikipedia, July 9, 2020. https://en.wikipedia.org/w/index.php?title=Honeycomb&oldid=966884736.
Graham. “An Introduction to Hexagonal Geometry | Hexnet.” Accessed July 12, 2020. https://hexnet.org/content/hexagonal-geometry.
Wigglesworth, V B. “The Structure and Deposition of the Cuticle in the Adult Mealworm, Tenebrio Molitor L. (Coleoptera),” 1934, 20.
Sun, Jiyu, and Bharat Bhushan. “Structure and Mechanical Properties of Beetle Wings: A Review.” RSC Advances 2, no. 33 (November 19, 2012): 12606–23. https://doi.org/10.1039/C2RA21276E.
“Benzene.” In Wikipedia, July 16, 2020. https://en.wikipedia.org/w/index.php?title=Benzene&oldid=968055875.
Béziau, Jean-Yves. “The Power of the Hexagon.” Logica Universalis 6, no. 1 (June 1, 2012): 1–43. https://doi.org/10.1007/s11787-012-0046-9.
O’Connor, JJ, and EF Robertson. “Perfect Numbers.” Maths History, 2020. https://mathshistory.st-andrews.ac.uk/HistTopics/Perfect_numbers/.
Crane, Keenan. “Discrete Differential Geometry: An Applied Introduction,” Carnegie Mellon University, April, 2020.







Comments