Coherent Structures: Part 2 – Gels
- Bill Beaver

- Aug 25, 2022
- 10 min read

Stylized gels [1]
During the months of June and July, I took a course offered by the Sante Fe Institute called “The Origins of Life.” [2] The course was a vast smorgasbord of ideas as the question: How did life emerge from non-life?” is one of the “hard” questions in science. What I learned from this course will continue to inform this and future posts.
In an earlier post [3] I talked about the different structures by the complex interactions of fluid turbulence acting within the confines of a planet. These structures have recognizable, repeatable, although sometimes rare shapes and features. They are also transient in time, having a beginning and an end. In complex system theory, this would be modeled as a far from equilibrium open dynamical system using some sort of energetic input to maintain coherence. In addition, these structures, although fluid, trap and filter particles suspended within the fluid. The dynamics of the system itself form a boundary and particles are either trapped inside or forced away. An example of this is how the fluid flow within Monterey Bay traps pollutants that are released inside a boundary region formed between the bay and the ocean. The creation of this boundary is what is called an emergent property of the fluid dynamics of the bay and ocean. The term “emergent property” is sometimes just hand waving about something little understood but in this case, it has been both theoretically modeled [4] and experimentally [5] verified.
Circularity in flow is created by feedback in the system, the state before is important to the next state. This implies causality which implies a one-way arrow of time, a clock. This is the start of a crude form of memory. As memory is a necessary component of (Turing [6]) computation, it would be interesting if an abiotic (nonliving) process could spontaneously perform computation. A bacterium can compute. It can “read” a chemical gradient and align itself to it, moving toward or away. I have found mentioned that hurricanes move towards a heat gradient in the ocean but I’ve not found any confirmation of this. On the contrary, hurricane size, strength, and direction are dependent on many factors but they have no agency of their own.
The fluid that I want to deal with from now on is water. Water is rarely ever pure, it always exists with other substances. At one extreme, water is one of the most powerful solvents, it can break up certain substances like salts into their atoms. Water can only hold so much dissolved material depending on density, pressure, and especially temperature. Dissolved materials can spontaneously particulate back into solid, sometimes growing crystals. [7] Particles that don’t dissolve are often negatively charged and water molecules, since they are polar, form a bi-layer (positive water to negative particle and then negative water to positive water) around them, protecting them further from dissolving. These particles are suspended in the water matrix. In fluid dynamics, these suspended particles move along as part of the fluid and can get trapped within the boundaries created by turbulent coherent structures. These particles can be filtered from the water, unlike dissolved particles. Suspended particles can also precipitate, for example, the salting of a soap solution to form flakes. [8] When the suspended particles are between 1 micron (1,000 nanometers or 1 millionth of a meter) and 10 nanometers in size the solution is called a colloid. With a colloid, the particles cannot be filtered out and can precipitate, a process called flocculation. [9] A special form of colloid is called a gel or hydrogel [10] when it contains water. Gels form a fourth state of matter, neither liquid nor solid. Gels have a semi-rigid structure in the form of a polymer network, long chains of molecules tangled together. Hydrogels can dry out from evaporation and then rehydrate when water returns.
The smallest bacterial cell is about 1 micron. Anything smaller than this and there is not enough room for DNA to replicate. This is why viruses, which can be much smaller, are unable to replicate without parasitism of a larger cell’s DNA machinery. This is also why viruses are not considered alive. The inside of a cell is considered a gel. If one wanted to watch all the processes of a cell one would need a resolution of about 10 nanometers. The gap in the synapse of a neuron, for instance, is about 20 nanometers. This is also the beginning of the quantum world as after less than 600 nanometers, quantum effects begin to show up. It was once believed that most bacteria were free living but most bacteria live bound together in a colloidal solution called a biological gel. This gel can form communities of many different species of bacteria and even include species of Eukaryotes, like fungi. In some bio gels, the polymer network holding the gel together is made up of extracellular DNA. [11] Biochemical processes take place within a certain scale within certain structures that can be classified as a gel. Hydrogels have abiotic properties like survival from dehydration/hydration cycles, self-assembly, and bi-layer protection that are also part of biological processes so this is important to understand for any clue of how life got started.
In 1827 the Scottish botanist Robert Brown was looking at live pollen grains when he saw small particles moving around inside. He spent several months researching this phenomenon. These particles, which he called molecules, he found in living and non-living matter. The particles moved when they were below a certain size, regardless of what they were made of. This is important as, at that time, living matter was assumed to possess a mystical force called a “life force,” which made life different from non-life, so Brown’s experiments were a major step forward for science. [12][13][14]
Between 1875 and 1922 a series of mathematicians, Weirstrass, Cantor, Peano, Lebesgue, Hausdorff, Koch, Sierpinski, and Besicovitch, began studying a series of curves with no tangents, functions that were continuous but not differentiable by calculus. These curves were considered curiosities, even monsters, and most mathematicians ignored them. In 1906 and again in 1926, Einstein showed that Brownian motion was related to diffusion in fluid mechanics and with this result, helped prove the atomic theory of matter. [15][16] In 1908, Jean Perrin won the Nobel Prize in Physics for his experiments with Brownian motion, again strengthening the atomic theory of matter. [17] In 1921, Norbert Wiener, inspired by Perrin’s work, defined Brownian motion as a type of random (stochastic) process, now called a Wiener Process. [18] Mathematically, Brownian Motion has three properties:
Independence – each iteration of the process requires no knowledge of the iteration before.
Gaussian – the random variable has a Gaussian distribution.
Isotropy – all paths are equally probable
Keep in mind that this is an idealization of how a larger particle is buffeted about by the fluctuations of millions of identical smaller particles in the surrounding fluid. The distance the particle travels during each movement is often considered constant while the direction is random, but both can be random.
It was realized that stochastic processes were important in and as dynamical systems. From 1942 onward, Kyoto Iṫoh described a stochastic calculus. [19] So now Stochastic Differential Equations have their place within the general theories of dynamic equations.

Fractal generation [20]
During the 1960s, the mathematician Benoit Mandelbrot was working for Bell Labs looking at random dropouts over phone lines. In 1971 he published a seminal work called Fractals Form Chance and Dimension. [21] A fractal is a geometric set in which the Hausdorff-Besicovtch (fractal) dimension is greater than or equal to the topological dimension. The topological dimension is our familiar Euclidean dimensions of 0 (point), 1 (line), 2 (plane), and 3 (volume)..., an integer. The fractal dimension is a scaling dimension since fractals are self-similar, they look the same no matter what scale. Take a line segment of length 1 and break it into N segments each 1/L in length. Do this forever. The fractal dimension is log(N)/log(1/L). This is not necessarily an integer, it is a rational number, a fraction, hence the word fractal. Mandelbrot notes that natural objects like clouds, mountains, coastlines or stock prices or Brownian motion, or telephone line noise are not smooth like Euclidean geometry but rough and also self-similar, they are all fractal. Fractals became very useful during the rapid breakthroughs in computer graphics during the 1980s and the fantasy worlds and renderings of movies today are partially a result of fractal geometry. Fractals show up in non-linear dynamics as deterministic chaos. The system goes into a state where the resulting output generates a fractal set.
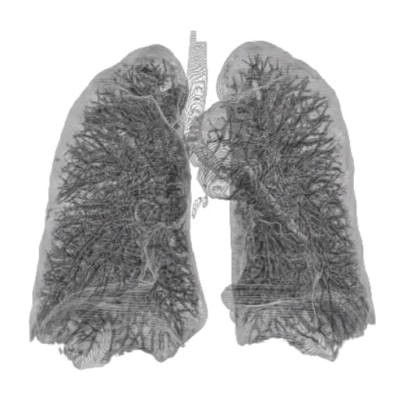
Fractal-like structure of a human lung [22]
Random processes are not geometrically self-similar but the process itself is, statistically. A Brownian random walk has a topological dimension of 1 since it is made up of straight lines, but a fractal dimension of 2. This means that a Brownian random walk will eventually visit every point on the plane. This shows up in biology as a random search, a major way a biological entity starts its search for food. Random search is a Brownian random walk as it is the most efficient way to search an unknown region. As information is gathered, the search transitions into something more directed. Brownian motion is a major source of kinetic energy in the colloidal state and increases in importance as the particles get smaller.

Brownian random walk [23]
Rheology is the experimental and theoretical study of colloids, gels, and glasses. Classical rheology is now called macrorheology as it was realized that completely different theoretical concepts and experimental techniques were needed to study materials in the 1-micron to 10-nanometer sweet spot. This is now called microrheology. [24]
In microrheology, a probe particle is placed in a material. It is watched as it moves by Brownian motion or the addition of gravity, or it has a directional force applied to it. By itself, the particle reaches a local equilibrium with the material but other forces on the probe, gravity and/or applied, pull the system out of equilibrium, and it becomes non-linear. In gels the state of the material is semi-solid, so elastic forces come into play as the probe particle pushes through the gel. [25] Also, particles in the gel sometimes stick to the probe particle instead of sliding past, hence the theoretical model of a gel is called “sticky spheres.” [26]
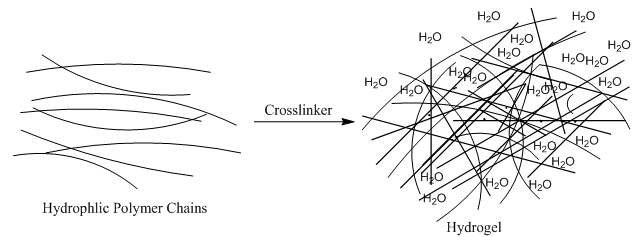
Polymer network [27]
Hydrogels can spontaneously form under certain conditions of concentration and energy sources. They can also collapse into a liquid. The whole system of a gel is a far from equilibrium transient structure, a coherent structure. A polymer is a long chain of molecules made up of like substructures. When a gel forms, polymer rods are created and these rods tangle together to form a polymer network. This holds the inner shape of a gel together and, along with the boundary layer, forms the structure of the gel. Polymer networks are theoretically modeled by the appropriate name “sticky rods.”
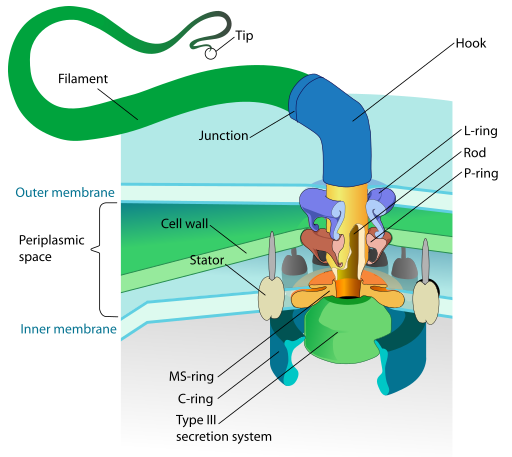
Flagellum as a molecular machine [28]
This is an example of self-assembly. Self-assembly is the way biology works as information molecules are read out, proteins are assembled, and then combined into complex molecular machines. Gels might hold a clue into how life got started. A collaboration of labs in Turkey and Singapore [29] used particles ranging from quantum dots (2 – 10 nm) to polymers (< 100 nm) to E Coli ( 1 – 2 microns) to human cells (10 – 100 microns) and a laser heat source. They were able to get the particles to spontaneously assemble together. Turning off the laser, the particles wandered apart. E Coli was the only particle that has autonomous mobility (flagella), human cells do not. This could be an important result as it shows another “life-like” property extending into nonlife.
The course I took on “The Origin of Life” was a real “Describing the Elephant” event with around 30 researchers giving sometimes competing results. Gels were merely hinted at being important, I am just running with it and expanding these ideas around a unifying concept of a coherent structure.
Craiyon LLC, “Craiyon, Formerly DALL-E Mini,” Craiyon, formerly DALL-E mini, accessed August 25, 2022, https://www.craiyon.com.
Sante Fe Institute, “Complexity Explorer,” accessed August 25, 2022, https://www.complexityexplorer.org/news/139-register-now-for-origins-of-life.
WJ Beaver, “Coherent Structures: Part 1, Clouds and Ocean Vortexes,” Emergent Thoughts, accessed August 25, 2022, https://wjbeaver.wixsite.com/mysite/post/coherent-structures-part-1-clouds-and-ocean-vortexes.
George Haller, “Lagrangian Coherent Structures,” 2014, 28.
Francious Lekien and Chad Coulliette, “A Lagrangian Coherent Structure of Surface Current in Monterey Bay,” ResearchGate, accessed June 15, 2022, https://www.researchgate.net/figure/a-A-Lagrangian-Coherent-Structure-of-surface-current-in-Monterey-Bay-Image-courtesy-of_fig3_327154971.
A. M. Turing, “On Computable Numbers, with an Application to the Entscheidungsproblem,” Proceedings of the London Mathematical Society s2-42, no. 1 (1937): 230–65, https://doi.org/10.1112/plms/s2-42.1.230.
Wikipedia, “Solubility,” in Wikipedia, April 20, 2022, https://en.wikipedia.org/w/index.php?title=Solubility&oldid=1083799249.
Wikipedia, “Salting Out,” in Wikipedia, April 22, 2022, https://en.wikipedia.org/w/index.php?title=Salting_out&oldid=1084111280.
Wikipedia, “Flocculation,” in Wikipedia, July 26, 2022, https://en.wikipedia.org/w/index.php?title=Flocculation&oldid=1100530078.
Wikipedia, “Hydrogel,” in Wikipedia, July 29, 2022, https://en.wikipedia.org/w/index.php?title=Hydrogel&oldid=1101148925.
Uta Böckelmann et al., “Bacterial Extracellular DNA Forming a Defined Network-like Structure,” FEMS Microbiology Letters 262, no. 1 (September 1, 2006): 31–38, https://doi.org/10.1111/j.1574-6968.2006.00361.x.
Brown, Robert. “A Brief Account of Microscopical. Observations Made in the Months of June, July, and August, 1827, on the Particles Contained in Tlze Pollen of Plants; and on the General Existence of Active Molecules in Organic and Inorganic Bodies.” The Philosophical Magazine and Annals of Philosophy, 1828.
Steven Lalley and Pers Mykland, “Brownian Motion” (Stochastic Processes II, University of Chicago, 2013);
Wikipedia, “Brownian Motion,” in Wikipedia, August 8, 2022, https://en.wikipedia.org/w/index.php?title=Brownian_motion&oldid=1103181543.
Albert Einstein, “Über Die von Der Molekularkinetischen Theorie Der Wärme Geforderte Bewegung von in Ruhenden Flüssigkeiten Suspendierten Teilchen,” in Wikipedia, 1905, https://en.wikipedia.org/w/index.php?title=%C3%9Cber_die_von_der_molekularkinetischen_Theorie_der_W%C3%A4rme_geforderte_Bewegung_von_in_ruhenden_Fl%C3%BCssigkeiten_suspendierten_Teilchen&oldid=1098847840.
Albert Einstein, “Investigations on the Theory of the Brownian Movement,” Dover, 1926, 11.
John Baptiste Perrin, “Mouvement Brownien et Réalité Moléculaire,” 1909, https://en.wikipedia.org/wiki/File:PerrinPlot2.gif.
Hossein Pishro-Nik, “Brownian Motion (Wiener Process),” in Probability, Statistics, and Random Processes (Kappa Research LLC, 2014), https://www.probabilitycourse.com/chapter11/11_4_0_brownian_motion_wiener_process.php.
Wikipedia, “Itô Calculus,” in Wikipedia, April 14, 2022, https://en.wikipedia.org/w/index.php?title=It%C3%B4_calculus&oldid=1082665064.
José Luis Llopis Fabra, Español: Fractal de Cesàro Con Ángulo de 85o Construido Con Un Sistema de Funciones Iteradas (IFS)., February 26, 2019, February 26, 2019, https://www.matesfacil.com/fractales/von-Koch/curvas-von-Koch-iteraciones-copo-anticopo-poligono-dimension-Cesaro-angulo-variantes-Minkowski.html, https://commons.wikimedia.org/wiki/File:Fractal_de_Ces%C3%A0ro_GIF.gif.
Benoit B. Mandelbrot, Fractals: Form, Chance and Dimension, (Brattleboro, Vermont: Echo Point Books & Media, 1977).
Andreas Heinemann, Human Lung. 3D Reconstruction, October 5, 2005, October 5, 2005, http://www.rad-zep.de, https://commons.wikimedia.org/wiki/File:Thorax_Lung_3d_(2).jpg.
Toshiyouri, 2 Dimension Random Walk of a Silver Adatom on a Ag(111) Surface, May 19, 2018, May 19, 2018, Own work, https://commons.wikimedia.org/wiki/File:2d_random_walk_ag_adatom_ag111.gif.
Roseanna N. Zia, “Active and Passive Microrheology: Theory and Simulation,” Annual Review of Fluid Mechanics 50, no. 1 (2018): 371–405, https://doi.org/10.1146/annurev-fluid-122316-044514.
The Physics of Gel-like Substances | Stanford University School of Engineering, accessed July 29, 2022, https://engineering.stanford.edu/magazine/physics-gel-substances.
C. Patrick Royall et al., “Real Space Analysis of Colloidal Gels: Triumphs, Challenges and Future Directions,” Journal of Physics: Condensed Matter 33, no. 45 (August 2021): 453002, https://doi.org/10.1088/1361-648X/ac04cb.
Sgmagill, Polymer Chains May Be Crosslinked in the Presence of Water to Form a Hydrogel. Water Occupies Voids in the Network, Giving the Hydrogel Its Characteristic Surface Properties, June 5, 2013, June 5, 2013, Own work, https://commons.wikimedia.org/wiki/File:Hydrogel_network.PNG.
LadyofHats, Flagellum Base Diagram-En.Svg - Wikimedia Commons, accessed August 25, 2022, https://commons.wikimedia.org/wiki/File:Flagellum_base_diagram-en.svg.
Ghaith Makey et al., “Universality of Dissipative Self-Assembly from Quantum Dots to Human Cells,” Nature Physics 16, no. 7 (July 2020): 795–801, https://doi.org/10.1038/s41567-020-0879-8.





Comments