Coherent Structures: Part 1, Clouds and Ocean Vortexes
- Bill Beaver

- Jun 18, 2022
- 14 min read
Updated: Aug 25, 2022

Morning Glory Cloud over Burke, Australia [1]
I didn’t know at first how to title this post, but I quickly found that my content was expanding so rapidly that this had to be broken into parts. Proper journalism says to not bury the lede, the most important and relevant part of an article, but as I look at my notes I’m not sure exactly what the lede is. On one level, this is my conclusion to the question: What is Mathematics? [2] At another level, this is a transformation to a new set of questions and inquiries. Many threads tie this article together, serendipitous wanderings through internet content space.
The Santa Fe Institute [3] started in 1984 as a workshop at Los Alamos by the physicist George Cowan and Murray Gell-Mann. By 1987 they had funding and a building at the top of Canyon Drive in Santa Fe, New Mexico, and a unifying research objective of promoting the study of complexity. [4] As a project, it at least seems to be fulfilling its goals. I don’t know enough yet about exactly how successful they are and since they are a private organization I would like more information on where they are getting their funding, but through their writings, podcasts, and other resources, I’ve run into many helpful ideas.
Sara Imari Walker [5] is a theoretical physicist at Arizona State University in Tempe, Arizona and Lee Cronin [6] is a chemist at the University of Glasgow, Scotland. In 1944 Erwin Schrödinger published a short book called What is Life? In it he asked a very simple but still intractable question:
“How can the events in space and time which take place within the spatial boundary of a living organism be accounted for by physics and chemistry?” [7]
78 years later, this question has not even begun to be answered. Walker wants to find a way to discover life in the Universe. She has realized that Schrödinger’s question about life on Earth has to be answered first before talking about life anywhere else. She has also realized that current physics lacks the language to talk about life, especially when talking about information. Life is so different from non-life that it needs its own category of complexity. Causation is a top-down process until you get to a level where something starts to push back. [8] Cronin is trying to create artificial life in his lab. Along the way, he is working on automating some of the steps in chemical discovery, has created a purely chemical computer, [9] a major breakthrough, and has discovered a way to measure chemical complexity, called “assembly theory.” I first found both through the Lex Fridman Podcast, [10][11][12][13] the Shawn Carroll Podcast (Walker), [14][15], and others (Cronin). [16]
Joel David Hamkins is a mathematician and philosopher of science at the University of Notre Dame in South Bend, Indiana. [17] I ran into a set of lectures he gave for the Michaelmas Term (Oct-Dec) at Oxford University in 2020. Because of the pandemic these lectures were given over Zoom and were recorded and released to the public on YouTube. [18] The lectures are based on a book of the same name. [19]
I started this blog in response to the question: Where are the new ideas? It was surprisingly difficult at first but gradually I have become happily overwhelmed. These three individuals severely broke my mind and this is another attempt to put together the pieces.
Coherence is defined as:
“The quality or state of cohering, especially a logical, orderly, and aesthetically consistent relationship of parts.” [20]
by “cohering” this means “to stick together,” somehow a coherent object holds together as a relationship of parts in some way. Coherence as a term has many specific definitions whether one is talking about classical physics or quantum physics or biology or neural science but for now, I want to look at two definitions of coherence, coherence as information, and coherence as structure. The following definition refers to coherence with respect to a scientific theory:
“Coherence is a property of an information set that boosts our confidence that its content is true ceteris paribus when we receive information from independent and partially reliable sources.” [21]
I’ll get back to coherence as information but first I want to talk about coherence as structure, especially in relation to Fluid Mechanics.
Humans are excellent at seeing patterns and categorizing what they see. Some are only useful in a cultural way, like seeing a man or rabbit on the surface of the Moon or the naming of groups of stars as constellations. Others form the basis of our science. In biology, living beings, are categorized into orders, families, genera, and species based on physical and behavioral characteristics and increasingly on differences in the structure of their DNA. There is a great debate between splitters and joiners, joiners accusing splitters of seeing differences where there are none. In atmospheric sciences, clouds are loosely categorized based on certain visual criteria and other well-known classifications such as hurricanes, tornadoes, and water spouts. In the ocean, there are currents, gyra, whirlpools, and eddies. One thing in common with all these is that they are not stable, they collapse and reform, and they have a birth and a death. This lifespan can be a few seconds or in the case of the North Atlantic Current, maybe hundreds of thousands of years. [22] one example on another planet is the Great Red Spot of Jupiter. The Great Red Spot was discovered in 1831 and might have been discovered as early as 1664 by John Hooke but there is controversy about that. [23] This “storm” on Jupiter is at least 200 years old and could be much older.

Great Red Spot of Jupiter [24]
Cloud patterns are general and fleeting but there are a few that are rare and extremely bizarre. One rare category is Altocumulus lenticularis. [25] This is a stacked lens-shaped cloud associated with the tops of mountains. These have been mistaken for flying saucers. I remember seeing one over the Santa Rita Mts during a summer rain, the dark storm behind it made it look like some forbidding invasion.

Altocumulus lenticularis [26]

Waiting for the saucer to land… [25]
Another category is roll clouds. These are long cylindrical clouds that look like 3D stripes from the air. These are rare and random except for one place on earth, northwestern Australia east of Darwin on the Gulf of Carpentaria and the small settlement of Burketown. [27] There, they are called Morning Glory Clouds. When I see these clouds I think that they look like 3D Turing Patterns. [28]
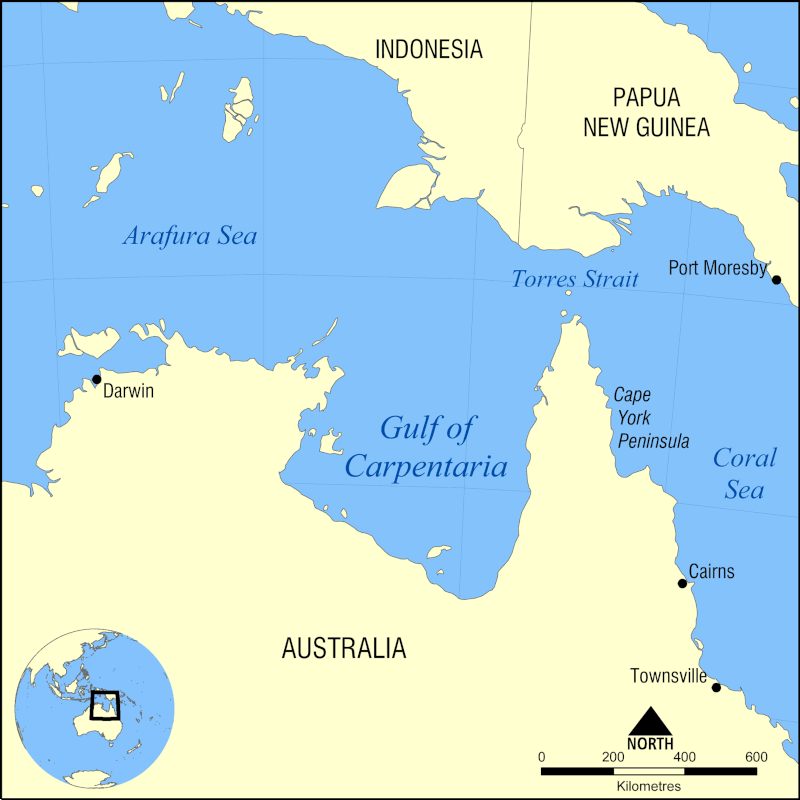
Gulf of Carpentaria [29]

Morning Glory Cloud on Land [1]

Morning Glory Clouds from the air [30]

Morning Glory Cloud Bands [31]
So how do we understand the processes that create coherent structures out of complex flows in air and water? Both Atmospheric and Oceanic sciences depend on a powerful tool called Fluid Mechanics. Fluid Mechanics models how fluid flows around a solid structure or how a solid structure moves through a fluid. There is also the problem of transport, how a larger object with weight, buoyancy, and drag, gets moved by fluid flow. One category of Non-Newtonion fluids is Bigham plastics. Wet flowing clay is an example of a Bingham plastic. Bingham plastics also show turbulence under certain conditions. [32]
In addition to co-inventing the calculus and the laws of motion, in 1687 Isaac Newton devoted part of the second volume of Philosophiæ Naturalis Principia Mathematica [33] to his experiments on fluid flow. Newton showed that over time a blob of fluid gets deformed at a certain rate, the strain rate and that the blob also resists deformation, called viscous stress. If the relationship between these two is linear, then the dynamics can be solved by mathematical analysis, if non-linear, much harder. For air and water, the relationship is very close to linear so the concept of a Newtonian or non-Newtonian fluid is an important one. [34]
For the next 100 years, three generations of mathematicians expanded on the Newton/Leibniz calculus. Leonhard Euler 1755 wrote out the full equations for a perfect fluid. [35] In 1788 Joseph-Louis Lagrange published Mécanique Analytique [36] which tied together all the treads of the current mathematics of mechanics. He also formulated a different but equivalent way to look at fluid dynamics. There is some controversy as I found that perhaps Euler also first formulated the Lagrangian method [37] but Lagrange brought all this together in a single body of work. The difference between what is now called the Eulerian method vs the Lagrangian method is this: with the Eulerian method you are standing on a rock looking at the river flow around it, with the Lagrangian method you are a particle in the river traveling around the rock. The Lagrangian method has been pretty intractable compared to the Eulerian method, even with modern computers. The visualizations created using the Eulerian method, the streaklines, correspond to what you see when you shine a laser through smoke or dye in a fluid flow. There is also the particle path, the trajectory of a single particle, and the velocity field which over time make up the streamlines. The Eulerian and Lagrangian methods have different concepts of velocity. The Eulerian measures off a fixed frame of reference while the other measures the velocity at a frame of reference to the particle. These can be transformed one into the other and form a dual way of looking at fluid flow. In the process of researching this post, I found several articles stating that the Lagrangian method is sort of a dead-end, but this is no longer true. [38]
Claude-Louis Navier 1822 first published a complete set of equations for fluid motion [39] and George Gabriel Stokes between 1842 – 1850 independently did the experimental research that confirmed Navier’s work. [40] The equation, now called the Navier-Stokes equation, is a set of non-linear partial differential equations with four independent variables. [41] Navier-Stokes is a complete description of fluid motion and adds to the Eulerian/Lagrangian methods the ideas of dissipation and diffusion (heat, energy, and particle flow.) Navier-Stokes has many quirks like being stubbornly non-linear and it may have solutions that aren’t ‘smooth’ essentially black holes. This is one of the major questions of mathematics in the 21st century and if Navier-Stokes is not ‘smooth’, what could this mean physically?
Newton’s concept of viscosity is a number associated with no physical dimension. Stokes thought he had found this number but it turned out to be wrong. In 1883 Osbourne Reynolds first started using a measure for viscosity, and by 1908 it was named after him. [42] Reynolds Number is a ratio, a measure that includes the physical properties of a fluid, the way a fluid resists deformation, and the size of an object. This hierarchy of size is important. For instance, how air flows around a person as opposed to how air flows around an insect as opposed to how air flows around a bacterium is very different as the Reynolds Number ranges from 106in humans to 10-6 in bacteria. [43] What does this mean? Flow around an object is either laminar or turbulent. Laminar flow means that the flow returns to the same structure downstream as it originally was downstream. Turbulence is much different, this forms the transient eddies, whirlpools, and clouds that are of interest here. A swimming human causes turbulence. Bacteria swim in water that is thick like honey so the flow is laminar. Also, at some point with a low Reynolds Number, dissipation and diffusion begin to become more important and the full Navier-Stokes model becomes needed.
Understanding and modeling turbulence is a holy grail for Fluid Mechanics. Here I quote myself from a previous post:
“In 1971 another one of Thom’s colleagues, David Ruelle along with Florence Takens published [44] in which they proposed that turbulence in fluid flow is chaotic. It took Ruelle a series of papers and a decade to get the physics community to accept this. A mathematical explanation of the onset of turbulence was one of Hilbert’s 10 problems for 20th Century mathematics to solve. This is still an unsolved problem and is now a 21st Century unsolved problem.” [45]
Turbulence is now accepted as an example of complexity. The name ‘Thom’ refers to the French topologist René Thom who first attempted a general theory of complexity. This was overhyped and failed to catch on and complexity theory today is a set of useful mathematical tools rather than a general theory. [46]

Satellite image of a vortex street of clouds in the lee of the Juan Fernández Islands. [47]

Look at the satellite image of a common turbulent structure, a vortex street. Next is a fluid mechanical model of an idealized vortex street using the Eulerian method. Notice how the blue and red particles mix in the vortexes forming alternate red and blue structures with a mix of both particles in the center. Notice that the vortexes in the model sort of fade out as they age. In reality, other processes destroy the structure. Modern computational fluid mechanics using the Eulerian method is beginning to produce beautiful visualizations of these structures but doesn’t give insight into how and why they form, and how particles move about and mix or sort. To do this requires looking at this from a particle view, the Lagrangian method, and a powerful tool from complexity theory called Lyapunov Exponents. In 2002, George Haller at the Swiss Federal Institute of Technology Zurich published Lagrangian coherent structures from approximate velocity data. [49]
Lagrangian Coherent Structures (LCS) are dynamic boundaries in the particle flow where a particle is either on a boundary or being attracted to a side of a boundary or is repelled by a side of a boundary. This boundary can either be a line in 2D space or a surface in 3D space. LCS is constructed using the Lagrangian method and a computational form of Lyapunov Exponents called Finite Time Lyapunov Exponents (FTLE). FTLE allows one to construct these boundaries and predict how these boundaries affect fluid flow. Computationally this is a two-step process in which the attracting and repelling boundaries are calculated separately. Visualization is needed. These are from a model of a double gyre:
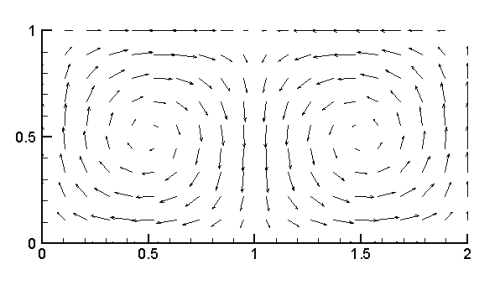
Velocity field using Euler Method [50]
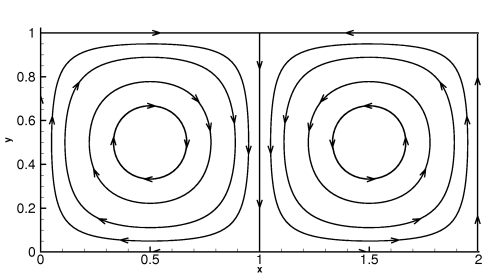
Streamline using Euler Method [50]
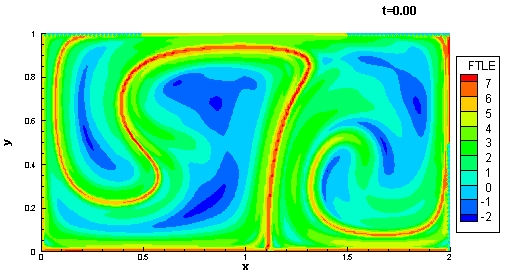
LCS with stable FTLE ridges in red [50]
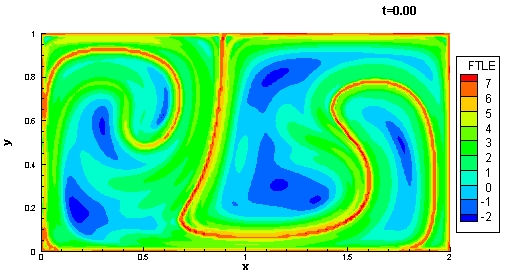
LCS with unstable FTLE ridges in red [50]
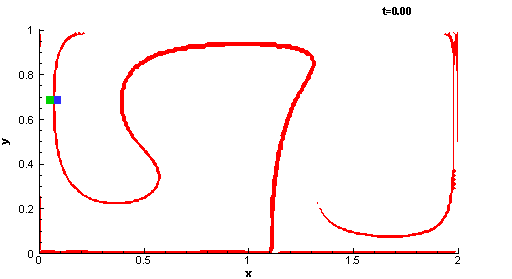
Animation of a trace of particles on either side of unstable ridges [50]
LCS has been used to study how pollutants get trapped in Monterey Bay, [51]
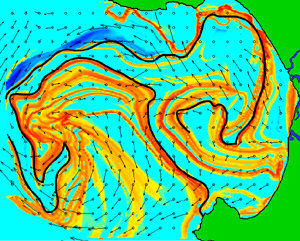
A Lagrangian Coherent Structure of surface current in Monterey Bay [52]
the paths of oil spills and humans lost at sea, [53] and here is an amazing model of how the undulations of a jellyfish creating an LCS that separates blobs of food from the surrounding water.
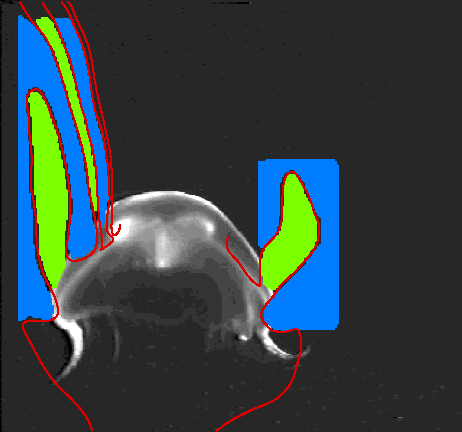
Jellyfish gathers food (LCS in red) [54]
LCS is just another way of “describing the elephant” which is a complex process. So what is a coherent structure? A list so far:
It is transient in time. It has a resolution and a dissolution. This transience is expressed in a series of oscillations or rotations that thus form a clock, a local version of time.
It is a complex dynamic process embedded within a complex dynamic process, a hierarchy of complexity.
There is also a hierarchy of scale involved.
It forms a boundary that sorts that which it encloses from what is outside. This looks to me very Maxwell’s Demonish, the entropy/information part is something I wish to explore further.
Coherent structures are made of physical stuff and thus obey the laws of physics.
I am curious about the term ‘memory’ I find occasionally used when talking about turbulence. What exactly does this mean? Memory again shows up in reaction-diffusion systems and Lee Cronin’s chemical computer, which is an array of Belousov–Zhabotinsky oscillating chemical reactions. Again, what exactly does ‘memory’ mean? And I need to understand replication better, starting with John Von Neumann’s paper. Time to end this and publish. Stay tuned.
ItsBC45, “The Morning Glory Cloud. A Phenomenon Where a Really Huge Line of Cloud Forms. It Looks Beautiful.,” Reddit Post, R/Interestingasfuck, November 6, 2020, www.reddit.com/r/interestingasfuck/comments/jpar0g/the_morning_glory_cloud_a_phenomenon_where_a/.
Bill Beaver, “What Is Mathematics?,” Emergent Thoughts, accessed May 28, 2022, https://wjbeaver.wixsite.com/mysite/post/what-is-mathematics.
Santa Fe Institute, “Santa Fe Institute,” accessed September 5, 2020, https://www.santafe.edu/.
John German, “History | Santa Fe Institute,” accessed May 28, 2022, https://www.santafe.edu/about/history.
ASU, “Emergence@ASU,” Emergence@ASU, accessed May 28, 2022, http://emergence.asu.edu/.
Cronin Group, “Digital Chemistry,” accessed May 28, 2022, https://www.chem.gla.ac.uk/cronin/.
Erwin Schrödinger, What Is Life? The Physical Aspect of the Living Cell. (Cambridge ; New York: Cambridge University Press, 1992).
Sara Imari Walker and Paul C. W. Davies, “The Algorithmic Origins of Life,” Journal of The Royal Society Interface 10, no. 79 (February 6, 2013): 20120869, https://doi.org/10.1098/rsif.2012.0869.
Parrilla-Gutierrez, Juan Manuel, Abhishek Sharma, Soichiro Tsuda, Geoffrey J. T. Cooper, Gerardo Aragon-Camarasa, Kevin Donkers, and Leroy Cronin. “A Programmable Chemical Computer with Memory and Pattern Recognition.” Nature Communications 11, no. 1 (March 18, 2020): 1442. https://doi.org/10.1038/s41467-020-15190-3.
Lex Fridman, “Lex Fridman Podcast,” accessed June 12, 2022, https://lexfridman.com/podcast/.
Lex Fridman, Sara Walker: The Origin of Life on Earth and Alien Worlds | Lex Fridman Podcast #198, 2021, https://www.youtube.com/watch?v=-tDQ74I3Ovs.
Lex Fridman, Lee Cronin: Origin of Life, Aliens, Complexity, and Consciousness | Lex Fridman Podcast #269, 2022, https://www.youtube.com/watch?v=ZecQ64l-gKM.
Lex Fridman, Alien Debate: Sara Walker and Lee Cronin | Lex Fridman Podcast #279, 2022, https://www.youtube.com/watch?v=SFxIazwNP_0.
Shawn Carroll, “Sean Carroll’s Mindscape Podcast – Sean Carroll,” accessed June 12, 2022, https://www.preposterousuniverse.com/podcast/.
Sean Carroll, “79 | Sara Imari Walker on Information and the Origin of Life – Sean Carroll,” accessed June 12, 2022, https://www.preposterousuniverse.com/podcast/2020/01/13/79-sara-imari-walker-on-information-and-the-origin-of-life/.
Foresight Institute, The First Programmable Turing Complete Chemical Computer | Lee Cronin, University of Glasgow, 2021, https://www.youtube.com/watch?v=ecdBDAfzHBM.
Joel David Hamkins, “Joel David Hamkins,” Joel David Hamkins, accessed May 4, 2022, http://jdh.hamkins.org/.
Joel David Hamkins, “Lectures on the Philosophy of Mathematics, Oxford Michaelmas Term 2020,” Joel David Hamkins (blog), October 7, 2020, http://jdh.hamkins.org/lectures-on-the-philosophy-of-mathematics-oxford-mt20/.
Joel David Hamkins, Lectures on the Philosophy of Mathematics (MIT Press, 2021), https://mitpress.mit.edu/books/lectures-philosophy-mathematics.
The Free Dictionary, “Coherence,” in The Free Dictionary, accessed March 26, 2022, https://www.thefreedictionary.com/coherence.
L. Bovens, “Solving the Riddle of Coherence,” Mind 112, no. 448 (October 1, 2003): 601–33, https://doi.org/10.1093/mind/112.448.601.
Paul Voosen, “Ancient Warming Threw This Crucial Atlantic Current into Chaos. It Could Happen Again,” 2020, https://www.science.org/content/article/ancient-warming-threw-crucial-atlantic-current-chaos-it-could-happen-again.
Marco Falorni, “The Discovery of the Great Red Spot of Jupiter,” British Astronomical Association, 1987.
Martin Perez, “Close-up of Jupiter’s Great Red Spot,” Text, NASA, July 12, 2017, http://www.nasa.gov/image-feature/jpl/pia21772/close-up-of-jupiter-s-great-red-spot.
Mark, “10 Very Rare Cloud Pictures,” Cool Things Collection | Collthings.Co.Uk (blog), December 15, 2021, https://www.collthings.co.uk/10-very-rare-cloud-pictures/.
WMO, “Altocumulus Lenticularis,” International Cloud Atlas, accessed June 3, 2022, https://cloudatlas.wmo.int/altocumulus-lenticularis.html.
Blythe Moore and Rob Mailer, “‘Morning Glory’ Rolls into the Gulf of Carpentaria,” ABC News, May 21, 2015, https://www.abc.net.au/news/2015-05-21/morning-glory-cloud-rolls-in-early-into-the-gulf-of-carpentaria/6486374.
Martin Skrodzki, Ulrich Reitebuch, and Eric Zimmermann, “Experimental Visually-Guided Investigation of Sub-Structures in Three-Dimensional Turing-like Patterns,” ArXiv:2006.16676 [Math, q-Bio], June 30, 2020, http://arxiv.org/abs/2006.16676.
Norman Einstein, “Morning Glory Cloud,” in Wikipedia, May 13, 2022, https://en.wikipedia.org/w/index.php?title=Morning_Glory_cloud&oldid=1087524489.
Mick Petroff, “A Morning Glory Cloud Formation between Burketown and Normanton, Australia.,” n.d., href="https://commons.wikimedia.org/w/index.php?curid=7556483".
Kent Wien, Stratocumulus (Morning Glory) Clouds, July 24, 2011, photo, July 24, 2011, https://www.flickr.com/photos/flyforfun/5972754080/.
Wilson, K. C., and A. D. Thomas. “Analytic Model of Laminar-Turbulent Transition for Bingham Plastics.” The Canadian Journal of Chemical Engineering 84, no. 5 (May 19, 2008): 520–26. https://doi.org/10.1002/cjce.5450840502.
Sir Isaac Newton, Philosophiae naturalis principia mathematica (Jussu Societatis Regiae ac typis Josephi Streater, prostant venales apud Sam. Smith, 1687).
Wikipedia, “Newtonian Fluid,” in Wikipedia, April 29, 2022, https://en.wikipedia.org/w/index.php?title=Newtonian_fluid&oldid=1085299521.
Sandro Caparrini, “The History of the Méchanique Analitique,” Lettera Matematica 2, no. 1 (June 1, 2014): 47–54, https://doi.org/10.1007/s40329-014-0043-3.
Joseph Louis Lagrange, Analytische Mechanik ...: Aus Dem Französischen Mit Einigen Anmerkungen und Erlauternden Zusätzen (Vandenhoeck und Ruprecht, 1797).
Sir Horace Lamb, Hydrodynamics (University Press, 1924).
James F Price and Woods Hole, “Lagrangian and Eulerian Representations of Fluid Flow: Kinematics and the Equations of Motion,” n.d., 90.
Sylvio R. Bistafa, “On the Development of the Navier-Stokes Equation by Navier,” Revista Brasileira de Ensino de Física 40, no. 2 (November 30, 2017), https://doi.org/10.1590/1806-9126-rbef-2017-0239.
Wikipedia, “Sir George Stokes, 1st Baronet,” in Wikipedia, May 4, 2022, https://en.wikipedia.org/w/index.php?title=Sir_George_Stokes,_1st_Baronet&oldid=1086211398.
H. Schlichting and K. Gersten, “Exact Solutions of the Navier-Stokes Equations.,” in Boundary-Layer Theory, 8th ed. (Springer, 2000), 83–112, http://www.amazon.com/Boundary-Layer-Theory-H-Schlichting/dp/3540662707.
N Rott, “Note on the History of the Reynolds Number,” Annual Review of Fluid Mechanics 22, no. 1 (January 1990): 1–12, https://doi.org/10.1146/annurev.fl.22.010190.000245.
H Berg, “Fluids and Swimming Low Reynold’s Number,” in And Random Walks in Biology, 2010.
David Ruelle and Floris Takens, “On the Nature of Turbulence,” Communications of Mathematical Physics 20 (1971): 167–92.
William Beaver, “Dynamic Systems and Modeling,” Emergent Thoughts, accessed June 4, 2022, https://wjbeaver.wixsite.com/mysite/post/dynamic-systems-and-modeling.
Rene Thom, Structural Stability and Morphogenisis An Outline of a General Theory of Models (W. A. BENJAMIN, INC, 1975).
Jeff Schmaltz, “A Swirl of Clouds over the Pacific” (NASA, August 19, 2013), https://earthobservatory.nasa.gov/images/81883/a-swirl-of-clouds-over-the-pacific.
Philip Oberdorfer, “The Beauty of Vortex Streets,” COMSOL (blog), accessed June 11, 2022, https://www.comsol.com/blogs/the-beauty-of-vortex-streets/.
G. Haller, “Lagrangian Coherent Structures from Approximate Velocity Data,” Physics of Fluids 14, no. 6 (June 2002): 1851–61, https://doi.org/10.1063/1.1477449.
Shawn Shaddon, “LCS Tutorial,” accessed June 10, 2022, https://shaddenlab.berkeley.edu/uploads/LCS-tutorial/overview.html.
Shawn C. Shadden et al., “The Correlation between Surface Drifters and Coherent Structures Based on High-Frequency Radar Data in Monterey Bay,” Deep Sea Research Part II: Topical Studies in Oceanography 56, no. 3–5 (February 2009): 161–72, https://doi.org/10.1016/j.dsr2.2008.08.008.
Francious Lekien and Chad Coulliette, “A Lagrangian Coherent Structure of Surface Current in Monterey Bay,” ResearchGate, accessed June 15, 2022, https://www.researchgate.net/figure/a-A-Lagrangian-Coherent-Structure-of-surface-current-in-Monterey-Bay-Image-courtesy-of_fig3_327154971.
Mattia Serra et al., “Search and Rescue at Sea Aided by Hidden Flow Structures,” Nature Communications 11 (May 26, 2020): 2525, https://doi.org/10.1038/s41467-020-16281-x.
Shawn C. Shadden, John O. Dabiri, and Jerrold E. Marsden, “Lagrangian Analysis of Fluid Transport in Empirical Vortex Ring Flows,” Physics of Fluids 18, no. 4 (April 2006): 047105, https://doi.org/10.1063/1.2189885.







Comments