What is Choice?
- Bill Beaver

- Sep 8, 2023
- 14 min read
Updated: Sep 15, 2023

El Farol Bar, Santa Fe, NM [1]
"Oh that place. It’s so crowded nobody goes there anymore." Yogi Berra
“You get pseudoorder when you seek order; you only get a measure of control when you embrace randomness.” N. N. Taleb [2]
Philosophy and Theory
to decide:
"Make a choice from a number of alternatives" [3]
to choose:
"Pick out or select (someone or something) as the best or most appropriate of two or more alternatives." [4]
The definitions above are two of the more non-circular I could find. I believe these can be used interchangeably, so I will stick with the term "choice." I am going to avoid the discussion of "free choice" and talk more about rational choice. To be rational in making choices is to work with facts and use logic. To be irrational one uses emotions, beliefs, and biases. Rational choice is supposedly how one should act. In economics, rational choice is assumed along with complete information and individual (selfish) maximization of results.
There are two primary forms of logic. Deductive logic starts with a true premise and works toward a conclusion that is assumed to be true. [5] This is exemplified by mathematical proof. Inductive reasoning starts with observation and does not result in a true conclusion, but rather a most probable conclusion. Rational choice, especially in Economics, is assumed to be deductive and how one 'should' act. Inductive reasoning comes in many "flavors," Inductive inference is a type of inductive logic in which a sample of a population infers conclusions about the population as a whole. Bayesian inference is inductive because you first assign a probability to a conclusion and then this probability changes as evidence becomes available. Bayesian inference is used when you don't have a sample population. [6]
Roland Fisher proposed statistical modeling as a mathematical concept in 1922. He assumed an infinite population that is to be sampled and was more interested in data from experiments and experimental design. This assumption of an infinite population is essentially the null hypothesis, a model is tested against this null hypothesis. The model was what was most important here, statistics reduced data to the parameters of the model, the numerical results. He termed this the "logic of inductive inference.." In 1933, Jerzy Neyman and Egon S. Pearson wrote an extension and critique of Fisher's ideas. They argued against the idea of an infinite population, rather than just a test against a null value they assumed that additional tests need to be made and a more correct starting point is against alternative competing hypotheses. Accepting or rejecting a hypothesis would also tell something about the alternative. Their biggest contribution was testing hypothesis, a test for whether a false hypothesis was wrongly deemed true, called size, and a test as to whether a true hypothesis was wrongly rejected as false, called power. First one must set the size, then optimize the power. This symmetry of testing Neyman and Pearson argued against the asymmetry of testing against a null. This they formalized mathematically as the "Fundamental Lemma of Neyman and Pearson," This led to a falling out between Pearson and Fischer. [7]
Mathematical probability and all its laws and theorems is a deductive mathematical structure. How this is applied to science and everyday life is contentious. Bayesian statistics and Classical "Frequentist" Statistics are two strands of statistical theory but both have concerns about the subjective vs. objective method of choice. 'Choice' comes in at every part of the process, from determining the type of experiment, if an experiment is possible, to picking what data to include and the structure of the included data. Any decision to accept or reject a hypothesis based on tests is fine, but where is the cutoff for the test? This again is a subjective choice. A 'P' value of 5% is a good consensus for many subjects, in phylogenetics, for instance, this value would be ludicrous. Neyman and Pearson argued for a more structured framework which Fisher rejected. By 1938 Neyman left England for the United States and Berkeley where he founded the first statistics department. [8] He named his statistical method, "Inductive Behavior.", 'behavior' in the sense of a decision, a choice, but one informed by induction:
"I consider it advisable to make the choice after examining (a) the relative undesirability of consequences of the various possible errors and (b) the frequencies, implied by that same model M, with which a given rule of behavior would lead to these different errors." [9]
Bayesian statistics represent an interpretation of probability where a belief about an event is based on prior knowledge of the event. Frequentist statistics represent an event based on the limit of many trials, a sampling from a larger population. The split in statistics between Bayesian and Frequentist methods also represents a split of agreement as to just what probabilities are. Do the probabilities represent a truly stochastic process or does it just seem stochastic because we are working with a sample of the complete process? [10] This is further conflicted by complex deterministic processes that can output what seems like stochastic results in the form of chaos. This is further contradicted by the notion of time, we can never recreate even a second ago for some kind of study. To me, this makes the argument moot. In practice, statistics is a set of methods gained from experience, computation allows any new method to be tested and refined or rejected by a population of users.
So far I have discussed choice in the context of making hypotheses in science so one might wonder what this means for trivial choices such as "Coke" or "Pepsi?" This may seem trivial to the chooser, but not so to manufacturers of the two products or to the distributors who have to know how much of each product to buy. So far all of the emphasis has been on the inner cognition of an individual. This implies a relationship between at least two individuals in the form of an exchange of some kind. A scientist wants a group of people to accept their research in the form of published papers, books, citations, grants, fame, etc. Acceptance also means that science moves forward, and a consensus of possible truth has been achieved. There is a one-to-many relationship between the makers of knowledge and the takers of knowledge, in this case, a community of makers (other scientists) and takers (publication, industry, and others.) For our consumer example, the makers of Coke or Pepsi have a one-to-many relationship with the takers of the product. The opposite assumption in both cases is that the relationship between taker and maker is strictly one-to-one. This, of course, is rarely true as is the assumption of complete information.
Game theory is the modeling of two or more choices between two or more individuals, henceforth called agents. For the simplest of games, two agents and two choices. These form what is called a payoff matrix, some measurement of the value of the choices. This models the interaction of choices between the agents. These are static simple models that nonetheless have a rich mathematical structure. One breakthrough was in 1950 when John Nash proved that static games can have an equilibrium, an optimal solution. [11] Much of the research in game theory is trying to understand how cooperation evolves, no static game could be devised where cooperation is a Nash equilibrium. Another breakthrough came in 1981 when Axelrod and Hamilton showed the most dismal of games, the Prisoner's Dilemma, when iterated, has a strategy that evolves towards cooperation. [12] This was the start of the study of dynamic games. This opened up the idea of a strategy, a way to change choices over time based on knowledge of the last choice. Another modeling technique is called agent-based or active agent modeling. Taking a cue from Cellular Autonoma, a population of agents is updated simultaneously based on some update rules.
How do humans actually choose? And how does the brain make choices? These are questions for psychology and neuroscience respectively.
Choice in Behavioral Economics
The fact that humans do not make purely rational decisions has been established in psychology and is taken as a set of constraints or bounds to rationality. Much of this work was done by Daniel Kahneman and Amos Tversky for which Kahneman won the Nobel Prize in Economics in 2002 (Tversky has died and the prize is only given to the living.) [13][14] One major cognitive constraint is short-term memory. Adult humans can hold on average 7 ideas in short-term memory, from 5 to 9 depending on the person. Short-term memory is constantly overwritten by new information coming in. Another is that given the probabilities of a set of choices, we will reduce this to the two best choices by averaging the probabilities rather than summing them. We choose losses differently than we choose gains. In addition, we have biases, and given variable outcomes, we don't always make an optimal choice.
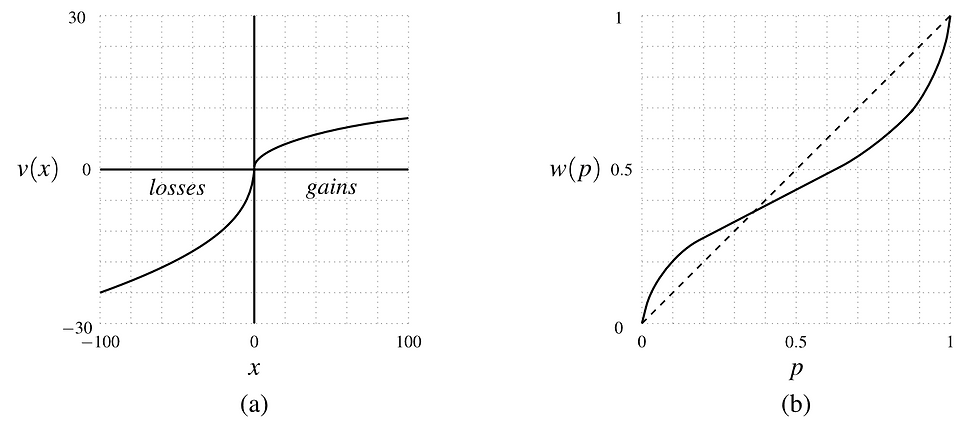
(a) Human choices of loss vs. gains.
(b) How we estimate probabilities and the actual estimate (dashed line.) [15]

An example of bias and variability in darts. Humans will accept results different than the optimum (upper left.) [15]
Rational choice was axiomatized mathematically by von Neumann and Morgenstern in 1944 [16] Herbert Simon in 1955 was the first to critique this view and proposed a theory of bounded rationality. [17] Simon won the Nobel Prize in economics in 1978. [18] Simon spent his whole career at Carnegie Mellon in Pittsburg in various departments but never in economics. His original interest was decision-making in corporations. He was an early advocate of computational approaches and a founder of the study of artificial intelligence and complexity theory. [19] For this, he won the Turing Award in 1975. [20] The Bounded Rationality of Simon and the Prospect Theory of Kahneman/Tversky is all part of what today is called Behavioral Economics. [21] Rational choice is now bounded and stochastic, but what to some might be considered human irrationality has been steadily made rational.
Choice in Neuroscience
You hear a sound and turn toward that sound. You see a green bird in a tree and you recognize a parrot. How does the brain process this to come up with the choice of "parrot?" A single coherent theory of how the brain makes choices does not exist. Bayesian statistics is used often but it has limitations. The brain processes sensory information (five senses) using different levels and processes which are both separate and highly interconnected. There are many layers before the actual decision process, sub-decisions between various inputs. Decisions are hierarchical, they cascade, and they are iterative in time. One thing that seems necessary is that there has to be some sort of conceptual boundary between the outside world and what humans call "the self." Does this mean that other animals have this sense of self? Do bacteria? There is a physical boundary in the form of the cell wall., does a bacterium "know" the difference? [22]
The El Farol Bar Problem
The El Farol Bar is a bar in Sante Fe, New Mexico. On Thursday nights they have a very popular Irish Music Night, The bar is not large, however, and the problem for a population of Irish music enthusiasts is whether to attend on a Thursday night or not given that a crowded bar will provide them with an unpleasant experience and a less crowded bar will not. If a person goes to the bar and it is crowded, they have an unpleasant experience, if the bar is not crowded, a good experience. If they decide to stay home, their experience is neutral. The only information they have is how many people were there the week before. In a paper written in 1994, Brian Authur showed that the two foundations of Expected Utility Theory, deductive reading, and complete information do not work for this particular problem, which could be thought of as the formation of a market for a scarce product. Inductive reasoning with incomplete information results in the average week-to-week fluctuation of patrons to the bar being equal to the bar's capacity. Deductively, the choice is a toss-up, an individual can either stay home every time or go every time, but collectively through inductive reasoning there is a better solution. An individual is given a set of rules to use as a means to a decision. This can be thought of as a learning strategy. Rules are based on information from one week past, from two, from three, etc. This can be thought of as memory [23] [1]. A way of looking at this problem is as an Agent-Based-Model (ABM.) Individual agents are programmed with a set of rules and constraints and all agents are updated simultaneously each iteration. One popular way of creating and visualizing these models is to use a specialized computer language called NetLogo. [24]
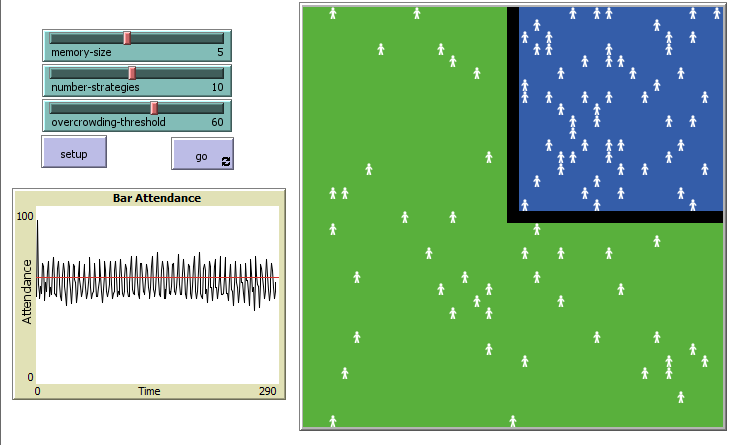
NetLogo implementation of the original El Farol Bar Problem. Default parameters after 290 iterations. Notice how attendance oscillates around the threshold value (red line). Tonight is a good night. [25]
ABMs hold the promise of performing experiments in research situations where the experimental manipulation of a population is difficult, expensive, or impossible. The parameter space can be large, a simple model like this one only has 3 parameters but a 4th, the population of all possible attendees, now set at 100, could easily be added. Exploration of the parameter space using brute force methods becomes time-consuming quite quickly. One solution is to use genetic algorithms to explore the parameter space. NetLogo provides both of these methods. [26] The EFBP as a model has a rich structure and has been analyzed as an n-person iterated game [27], a discrete dynamical system [28][29], a dynamic network [30], and Bayesian Inference. [31]
In 1997, the EFBP model was generalized to what is called the Minority Game. [32] Minority in the sense that a minority of agents win each iteration. This model took off in the statistical mechanics community in particular. As of 2003, one site lists 126 papers written about the model. [33] The model has been found useful in writing algorithms for the allocation of electricity in an electrical network and for the allocation of memory resources in computer networks. [34] Statistical mechanics research has shown it to be related to the theory of condensed matter, the formation of gels and glasses. The Minority Game has been found to be more general than these dynamical models as it doesn't have the physical constraints that the models of physical processes have. [35]
I am not convinced as yet that the methods of using ABMs in an experimental setting have been properly worked out. What an ABM can do is provide insight into a process. So what insight has the El Farol Bar Problem given to the issue of choice?

Computational resources are needed but peak at a low level [36]
In the graph above, points along the curve represent various cognitive models of choice for the EFBP from purely random to Arthur's inductive reasoning with minimal computational effort, to a model of maximal computational effort to pure neoclassical rationality. Notice that Athur's model hits a sweet spot and results actually worsen as computational power increases. This works the same for increased memory, how many performances an agent can remember the attendance. [37] Another result is that as the number of strategies picked goes up, the spread of the variation between maximal attendance and minimal attendance goes down. Arthur's inductive model works within the bounds of human short-term memory and becomes more efficient as the heterogeneity of strategies increases, regardless of the cognitive effort of maintaining the various strategies. [38][39]
Etic and Emic, Agent-based Models
Etic and emic are terms in the social sciences about two ways of looking at a culture. Emic relates to a person in a culture, how they feel and believe, and how these feelings and beliefs determine the choices they make. Etic is a viewpoint from outside of a culture looking in, a culture being the composite result of these emic choices. ABMs can provide insight into the nature and structure of choices. [40] What has been shown are examples of economic choice. Social choice is a little different. Economic choice is a social choice but the reverse may not be true despite the clamor of economists and industry to make every human interaction a market. Also, in the study of past or present non-capitalist non-Western cultures, do economic capitalist ideologies get in the way? The idea that every exchange has to have a utility might seem strange in some societies. [41] One advantage of these multi-agent models is that the payoffs come from the collective actions of a set of individual rules. These rules can be termed emic, they reside inside of the 'mind' of the agent. Real humans do not know what even the person closest to them is thinking, let alone someone from a distant past. The results of these collective individual actions form the etic, the structure in which the individual actions reside. The remains of a human culture in the form of artifacts can be pieced together to provide insight into the culture. These artifacts are also the result of years of collective choices. These choices can form the beginning of a narrative of how they might have thought. A narrative informed by the understanding of choice. [42][43]
Veisdal, Jørgen. “The El Farol Bar Problem.” Medium, June 9, 2021. https://www.cantorsparadise.com/the-el-farol-bar-problem-a60205dd3f86.
Taleb, Nassim Nicholas Nicholas. Antifragile: Things That Gain from Disorder. Reprint edition. New York: Random House Publishing Group, 2014.
Oxford Languages. “Oxford Languages and Google.” Accessed August 13, 2023. https://languages.oup.com/google-dictionary-en/.
Wikipedia. “Deductive Reasoning.” In Wikipedia, July 10, 2023. https://en.wikipedia.org/w/index.php?title=Deductive_reasoning&oldid=1164762581.
Wikipedia. “Inductive Reasoning.” In Wikipedia, July 30, 2023. https://en.wikipedia.org/w/index.php?title=Inductive_reasoning&oldid=1167844012.
Hawthorne, James. “Inductive Logic.” In The Stanford Encyclopedia of Philosophy, edited by Edward N. Zalta, Winter 2020. Metaphysics Research Lab, Stanford University, 2020. https://plato.stanford.edu/archives/win2020/entries/logic-inductive/.
Lenhard, Johannes. “Models and Statistical Inference: The Controversy between Fisher and Neyman–Pearson.” The British Journal for the Philosophy of Science 57, no. 1 (March 2006): 69–91. https://doi.org/10.1093/bjps/axi152.
Lehmann, E. L. “Neyman’s Statistical Philosophy.” In Selected Works of E. L. Lehmann, edited by Javier Rojo, 1067–73. Selected Works in Probability and Statistics. Boston, MA: Springer US, 2012. https://doi.org/10.1007/978-1-4614-1412-4_90.
Neyman, J. “‘Inductive Behavior’ as a Basic Concept of Philosophy of Science.” Revue de l’Institut International de Statistique / Review of the International Statistical Institute 25, no. 1/3 (1957): 7–22. https://doi.org/10.2307/1401671.
Romeijn, Jan-Willem. “Philosophy of Statistics.” In The Stanford Encyclopedia of Philosophy, edited by Edward N. Zalta and Uri Nodelman, Winter 2020. Metaphysics Research Lab, Stanford University, 2020. https://plato.stanford.edu/archives/win2020/entries/statistics/.
Nash, John F. “Equilibrium Points in N-Person Games.” Proceedings of the National Academy of Sciences 36, no. 1 (January 1, 1950): 48–49. https://doi.org/10.1073/pnas.36.1.48.
Axelrod, R., and W. D. Hamilton. “The Evolution of Cooperation.” Science 211, no. 4489 (March 27, 1981): 1390–96. https://doi.org/10.1126/science.7466396.
Kahneman, Daniel, and Amos Tversky. “Prospect Theory: An Analysis of Decision Under Risk.” Ecometrica 47, no. 2 (1979): 263–92. https://doi.org/10.1142/9789814417358_0006.
Kahneman, Daniel. “Nobel Speech - The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 2002.” NobelPrize.org. Accessed August 28, 2023. https://www.nobelprize.org/prizes/economic-sciences/2002/kahneman/lecture/.
Wheeler, Gregory. “Bounded Rationality.” In The Stanford Encyclopedia of Philosophy, edited by Edward N. Zalta. Metaphysics Research Lab, Stanford University, 2020. https://plato.stanford.edu/archives/fall2020/entries/bounded-rationality/.
Von Neumann, John, and Oskar Morgenstern. Theory of Games and Economic Behavior. Princeton University Press, 1944. https://press.princeton.edu/books/paperback/9780691130613/theory-of-games-and-economic-behavior.
Simon, Herbert A. “A Behavioral Model of Rational Choice.” The Quarterly Journal of Economics 69, no. 1 (1955): 99–118. https://doi.org/10.2307/1884852.
Simon, Herbert. “Nobel Lecture - The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 1978.” NobelPrize.org, 1978. https://www.nobelprize.org/prizes/economic-sciences/1978/simon/lecture/.
Bettis, Richard A., and Songcui Hu. “Bounded Rationality, Heuristics, Computational Complexity, and Artificial Intelligence.” SSRN Scholarly Paper. Rochester, NY, September 18, 2018. https://papers.ssrn.com/abstract=3251489.
Simon, Herbert. “Herbert A. Simon - A.M. Turing Award Laureate,” 1975. https://amturing.acm.org/award_winners/simon_1031467.cfm.
Laibson, David, and John A. List. “Principles of (Behavioral) Economics.” American Economic Review 105, no. 5 (May 1, 2015): 385–90. https://doi.org/10.1257/aer.p20151047.
Zaidel, Adam, and Roy Salomon. “Multisensory Decisions from Self to World.” Philosophical Transactions of the Royal Society B: Biological Sciences 378, no. 1886 (August 7, 2023): 20220335. https://doi.org/10.1098/rstb.2022.0335.
Arthur, W. Brian. “Inductive Reasoning and Bounded Rationality.” The American Economic Review 84, no. 2 (1994): 406–11.
Wilenski, Uri. “NetLogo Home Page.” Accessed November 15, 2020. https://ccl.northwestern.edu/netlogo/.
Rand, William, and Uri Wilenski. “El Farol NetLogo Model.” NetLogo Models Library:, 2007. https://ccl.northwestern.edu/netlogo/models/ElFarol.
Stonedahl, Forrest. “Genetic Algorithms for the Exploration of Parameter Spaces in Agent-Based Models.” NORTHWESTERN UNIVERSITY, 2011. https://www.proquest.com/openview/e5a7ad809d3b5f3ed5ccf42197ad7e79/1?pq-origsite=gscholar&cbl=18750.
Szilagyi, Miklos N. “The El Farol Bar Problem as an Iterated N-Person Game.” Complex Systems 21, no. 2 (June 15, 2012): 153–64. https://doi.org/10.25088/ComplexSystems.21.2.153.
St Luce, St. Luce. “Analyzing the El Farol Bar Problem as a Complex Dynamical System.” State University of New York, 2021. https://www.proquest.com/openview/552be025bd4d85e6111272f00e81cb7e/1?pq-origsite=gscholar&cbl=18750&diss=y.
St. Luce, Shane, and Hiroki Sayama. “Phase Spaces of the Strategy Evolution in the El Farol Bar Problem.” In The 2020 Conference on Artificial Life, 558–66. Online: MIT Press, 2020. https://doi.org/10.1162/isal_a_00339.
St. Luce, Shane, and Hiroki Sayama. “Network-Based Phase Space Analysis of the El Farol Bar Problem.” Artificial Life 27, no. 2 (May 2, 2021): 113–30. https://doi.org/10.1162/artl_a_00347.
Zambrano, Eduardo. “When Boundedly Rational Behavior Is Rationalizable: The Case of the El Farol Problem,” n.d.
Challet, D., and Y. -C. Zhang. “Emergence of Cooperation and Organization in an Evolutionary Game.” Physica A: Statistical Mechanics and Its Applications 246, no. 3 (December 1, 1997): 407–18. https://doi.org/10.1016/S0378-4371(97)00419-6.
Challet, Damian. “Articles Related to the Standard Minority Game,” 2003. https://web.archive.org/web/20141010122506/http://www3.unifr.ch/econophysics/minority/papers.html.
Hu, Miao, Zixuan Xie, Di Wu, Yipeng Zhou, Xu Chen, and Liang Xiao. “Heterogeneous Edge Offloading With Incomplete Information: A Minority Game Approach.” IEEE Transactions on Parallel and Distributed Systems 31, no. 9 (September 2020): 2139–54. https://doi.org/10.1109/TPDS.2020.2988161.
Challet, Damien, Matteo Marsili, and Gabriele Ottino. “Shedding Light on El Farol.” Physica A: Statistical Mechanics and Its Applications 332 (February 2004): 469–82. https://doi.org/10.1016/j.physa.2003.06.003.
Rand, William. “The El Farol Bar Problem and Computational Effort: Why People Fail to Use Bars Efficiently,” n.d.
Baccan, Davi, Luis Macedo, and Elton Sbruzzi. “Is the El Farol More Efficient When Cognitive Rational Agents Have a Larger Memory Size?” In 2014 IEEE International Conference on Systems, Man, and Cybernetics (SMC), 39–44, 2014. https://doi.org/10.1109/SMC.2014.6973881.
Collins, Andrew J. “Strategic Group Formation in the El Farol Bar Problem.” In Complex Adaptive Systems: Views from the Physical, Natural, and Social Sciences, edited by Ted Carmichael, Andrew J. Collins, and Mirsad Hadžikadić, 199–211. Understanding Complex Systems. Cham: Springer International Publishing, 2019. https://doi.org/10.1007/978-3-030-20309-2_9.
Lus, Hilmi, Cevat Onur Aydin, Sinan Keten, Hakan Ismail Unsal, and Ali Rana Atilgan. “El Farol Revisited.” Physica A: Statistical Mechanics and Its Applications 346, no. 3–4 (February 2005): 651–56. https://doi.org/10.1016/j.physa.2004.09.040.
Chen, Shu-Heng, and Ying-Fang Kao. “Herbert Simon and Agent-Based Computational Economics.”In Minds, Models and Milieux: Commemorating the Centennial of the Birth of Herbert Simon, edited by Roger Frantz and Leslie Marsh, 113–44. Archival Insights into the Evolution of Economics. London: Palgrave Macmillan UK, 2016. https://doi.org/10.1057/9781137442505_7.
Zafirovski, Milan. “Social Exchange Theory under Scrutiny: A Positive Critique of Its Economic-Behaviorist Formulations.” Electronic Journal of Sociology, January 1, 2005.
Harris, Marvin. “History and Significance of the EMIC/ETIC Distinction.” Annual Review of Anthropology 5, no. 1 (October 1976): 329–50. https://doi.org/10.1146/annurev.an.05.100176.001553.
Bayman, James M. “Emic and Etic Perspectives on the History of Archaeology.” Reviews in Anthropology 29, no. 4 (February 1, 2001): 361–77. https://doi.org/10.1080/00988157.2001.9978266.







Comments